I’ve always wondered about the magic which powers peer-to-peer file sharing. How you were able to quickly download some data by downloading small parts of it from many connected peers was something I didn’t quite understand. Now, many years later I’m using the same principles while working on a peer-to-peer network for Nuts, a disruptive decentralized information exchange network for health care providers. It was quite the Aha-erlebnis.

A use case for Merkle trees

An important part of retrieving a piece of data from a peer-to-peer network is finding out who has it (so you can get it from them) and being able to verify that they actually sent what you asked (and not a virus). The key here is (of course) hashing.

Hash trees in file sharing

First of all, how do you ask for the piece of data? File names can be changed, so they aren’t a very good way to address it (when I ask for furry_kitten.mov you might serve me something different than I’d expect). It’s much safer to ask for it by specifying its hash, which guarantees us we’re talking about the same piece of data.

Now what if the data was chopped up in somewhat equal blocks, and we have the hash of each individual block? Then we can ask others “hey, do you have the data for block identified by hash XYZ?”. That’d spread the load on multiple peers and if one of them goes down, we can just ask someone else for that particular block. If we want to check if we really have all blocks we can just calculate the hash of all hashed blocks.

Now we have something called a hash list, a list of hashes which are hashed again to get a single hash representing the list.

Merkle trees

But what if the piece of data is so large that calculating the hash over all block hashes becomes too expensive? Then we can use a Merkle tree, which is a binary tree where each node is a hash over its child nodes. That way we can efficiently recalculate our hash all the blocks we have by rehashing just the part of the tree that changed:

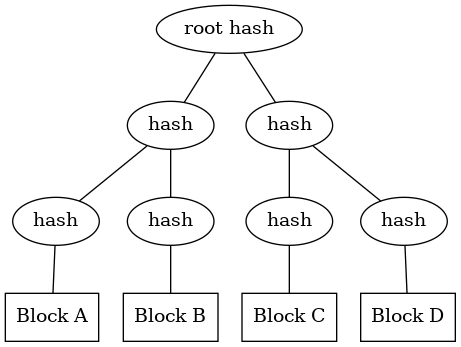
To calculate the root hash of this (fixed) tree, you’d effectively be doing:

root = hash(hash(hash(a) + hash(b)), hash(hash(c) + hash(d)))

An implementation in Go

For the complete example refer to golang-merkle-tree on Github.

We’ll be using SHA-128 for our hash function:

type Hash [20]byte

func (h Hash) String() string {
	return hex.EncodeToString(h[:])
}

func hash(data []byte) Hash {
	return sha1.Sum(data)
}

Which is used to hash our data blocks:

type Hashable interface {
	hash() Hash
}

type Block string

func (b Block) hash() Hash {
	return hash([]byte(b)[:])
}

We’ll also need an empty block (in case the number of data blocks is odd) which will result in a zeroed hash:

type EmptyBlock struct {
}

func (_ EmptyBlock) hash() Hash {
	return [20]byte{}
}

Nodes will hash the concatenated hashes of their children:

type Node struct {
	left  Hashable
	right Hashable
}

func (n Node) hash() Hash {
	var l, r [sha1.Size]byte
	l = n.left.hash()
	r = n.right.hash()
	return hash(append(l[:], r[:]...))
}

Then we can build the Merkle tree, from the bottom up. The function is recursive and the returned slice contains a single entry which is the Merkle root node.

func buildTree(parts []Hashable) []Hashable {
	var nodes []Hashable
	var i int
	for i = 0; i < len(parts); i += 2 {
		if i + 1 < len(parts) {
			nodes = append(nodes, Node{left: parts[i], right: parts[i+1]})
		} else {
			nodes = append(nodes, Node{left: parts[i], right: EmptyBlock{}})
		}
	}
	if len(nodes) == 1 {
		return nodes
	} else {
		return buildTree(nodes)
	}
}

And a helper function to print the tree:

func printTree(node Node) {
	printNode(node, 0)
}

func printNode(node Node, level int) {
	fmt.Printf("(%d) %s %s\n", level, strings.Repeat(" ", level), node.hash())
	if l, ok := node.left.(Node); ok {
		printNode(l, level+1)
	} else if l, ok := node.left.(Block); ok {
		fmt.Printf("(%d) %s %s (data: %s)\n", level + 1, strings.Repeat(" ", level + 1), l.hash(), l)
	}
	if r, ok := node.right.(Node); ok {
		printNode(r, level+1)
	} else if r, ok := node.right.(Block); ok {
		fmt.Printf("(%d) %s %s (data: %s)\n", level + 1, strings.Repeat(" ", level + 1), r.hash(), r)
	}
}

Finally, to build and print the tree:

func main() {
	printTree(buildTree([]Hashable{Block("a"), Block("b"), Block("c"), Block("d")})[0].(Node))
}

Outputs (numbering indicates tree depth):

(0)  b03975daeeae4fdb57ca2dabeadb1fdb159969cf
(1)   0056540ac6237d0263dd0faa45c71c73bc480f34
(2)    86f7e437faa5a7fce15d1ddcb9eaeaea377667b8 (data: a)
(2)    e9d71f5ee7c92d6dc9e92ffdad17b8bd49418f98 (data: b)
(1)   9bb287f18d2229d59c6bf5e8fe324f1b5cda56d4
(2)    84a516841ba77a5b4648de2cd0dfcb30ea46dbb4 (data: c)
(2)    3c363836cf4e16666669a25da280a1865c2d2874 (data: d)